凹坑尺寸非常重要！会直接影响喷丸强度和覆盖率。喷丸强度和凹坑的尺寸是直接成比例的。覆盖率随凹坑尺寸增大（其他条件相同时）。因此，凹坑的尺寸是非常重要的。凹坑尺寸的控制取决于已知的（a）尺寸，（b）尺寸的影响因素，（c）影响凹坑尺寸的喷丸方法。

 

 

图1低覆盖率下凹坑的形状

 

    典型的凹坑如图1所示。形状为近似圆形。如图中A处标注的一个凹坑，将其“等价为圆形”，如图中B处直径为d的圆形。当覆盖率和凹坑深度模型化时可假定为等价圆形。

    本文是对集中影响凹坑尺寸的因素进行定量分析。希望不喜爱数学的读者不会因为引入这些必要的方程式而离开。常见的计算程序，如Excel，允许在这些方程式中插入已知的值。例如，在Excel中计算凹坑直径时，A1中插入已知的丸料直径，A2中已知的凹坑直径，以及A3中等式：=（A2-(A1^2-A2^2)^0.5）/2。此等式与后续文中的等式（1）相同。

    丸料尺寸与凹坑直径

    丸料尺寸与喷丸引起的凹坑的尺寸存在线性关系——其他条件相同。实际观察与理论分析都能得出这个确定的结论。标准喷丸会引起凹坑，其直径大约为丸料的30~50%。因此，我们可以推测出凹坑的尺寸范围——因为我们已经知道使用的丸料的直径。

    图2所示为，当使用直径为D的铸钢丸时，推测的凹坑直径d的范围。SAE名义丸料尺寸说明这是最常见的尺寸参数。可以看出可能会遇到凹坑直径有巨大的范围。假设d是D的40%，则：凹坑直径在微米级别大致与使用丸料的SAE数值相同。

    例如，S110丸料产生凹坑直径大概为110微米，而S460丸料通常产生凹坑直径大约为460微米——1微米等于1um。

 

图2 使用铸钢丸产生凹坑直径的常用范围

 

凹坑深度，h

    凹坑深度h，取决于丸料直径D和凹坑直径d。如果假设凹坑是圆形且丸料是球形，则h，d和D之间的关系为：

    h=[D-(D2-d2)0.5]/2，d

    举例：如果D=110um，d=44um，h=4.6um，h是d的11%。图3所示为凹坑深度与凹坑直径的关系。D为100，则h是D的百分数。如果凹坑直径是D的20%，则深度仅为D的1%。即使凹坑直径是D得60%，凹坑深度也仅为D的10%。d/D的比值百分数如图中标示为30,40和60%。

 

 

图3 凹坑深度与凹坑直径的一般比例关系

 

凹坑直径和深度的预测

    我们可以预测由喷丸引起的凹坑直径和深度——假如已知几个控制因素。控制因素为：丸料直径，速度，密度，以及恢复系数。除恢复系数所有因素都是熟悉的。

    可以证明恢复系数是喷丸参数中最重要的。它可以说明当丸料撞击工件时有多少能量保留在工件中。假设丸料从一个固定高度h1掉落在平直的工 件上。它会弹起到一个高度h2，那么恢复系数e为：

    e=√（h2/h1）     （2）

    如果h2是h1的一半 ，那么丸料就损失了一半的能量。e的值就为0.71。如果h2等于h1（e=1） ，那么丸料在冲击过程中就没有损失能量，也不会产生凹坑。

    等式（3）说明几个因素对凹坑直径的影响。

    d=0.02284*D*(1-e2)0.25*p0.25*v0.5/B0.25      （3）

  p为丸料密度，v为喷丸速度，B为工件布氏硬度。

当使用公制单位时——v的单位为ms-1，p单位为kgm-3，适当的系数是0.02284。

A	B	C
4	K	0.02284
5	丸料直径-mm	0.100
6	恢复系数-e	0.71
7	密度-Kgm^-3	7860
8	速度，v-ms^-1	85
9	工件布氏硬度	300
11
12	凹坑直径，d-mm	0.040
13	凹坑深度，h-mm	0.004

图4 凹坑直径和深度预测表

 

    等式（3）很复杂，很难去定量体现。较简单的方法是将等式体现在Excel表格中。只要简单的按一个按钮就能看见各因素值的改变对结果的定量影响。如图4所示的表格就包含了基于等式（1）的凹坑深度的计算。将已知的值输入黄色空格中，结果就会在绿色空格中出现。K值和e值是确定的（除非有不同的、已测定的值）。当钢丸冲击到钢工件时，e的值为0.71。可以根据需要复制使用此表格。

    使用表格计算方法的好处是，可以简单定量分析各因素值的改变对结果的影响。通过在同样的表格中复制图4会使分析更容易。例如，如图1所示凹坑的直径变化大约为1/2。对于给定的样品，工件硬度、恢复系数和丸料密度都是常量。这样就仅有丸料直径和喷丸速度可能会引起凹坑直径的改变。使用图4中给出得初始值，为了将预测的凹坑直径减半，速度从85m/s下降到21m/s。丸料直径也只能减半（为了将预测的凹坑直径减半）。铸钢丸规格可以允许直径变化大于1/2。因此，可以合理的提出图1中凹坑直径的变化很大部分是因丸料直径变化引起的。

喷丸角度对凹坑形状的影响

    丸料很少会垂直的撞击在工件上。通常会以一个角度θ撞击到表面，如图5所示。丸流的分散，工件表面的弯曲以及丸流撞击表面的角度，都会使得θ减小并小于90°。喷丸角度对于喷丸强度和凹坑尺寸都有较大的影响。当θ等于90°时，球形丸料会产生一个圆形的凹坑。如果θ小于90°，则凹坑是椭圆的。

    图6所示为，一个丸料以45°（从右到左）撞击在纯钢工件表面产生的椭圆形凹坑。纯钢是非常有用的研究型材料，因为其突出的塑性变形性能——如图6中左侧的凹痕所示。

 

图5丸料以角度θ撞击在工件表面的A处

 

 

图6丸料以45°撞击在平直纯钢表面产生的椭圆凹坑

 

    由长轴和短轴之比来定义椭圆度，a/b。较早之前就已描述过初期的椭圆形凹坑。

喷丸角度对喷丸强度的影响

    研究经验表明，喷丸角度一同样的方式影响喷丸强度和凹坑深度，如图7所示。他们都与sinθ1.5成反比。

 

图7随着喷丸角度的改变，喷丸强度和凹坑深度的变化

 

    例如，当θ=60°，喷丸强度值是θ为90°时的80%。而到20°时，仅为20%。这说明，喷丸时应尽量使喷丸角度接近90°。

喷丸角度对凹坑尺寸和覆盖率的影响

    凹坑尺寸可以由其边缘圈定的平面面积定义。对于一个圆形的凹坑，尺寸即为圆形的面积πd2/4。对于椭圆形凹坑，尺寸即为椭圆面积πab/4。早期研究经验表明，喷丸角度和凹坑面积之间存在一定关系。这种关系就是，凹坑面积与sinθ成反比，如图8所示。相关的覆盖率与sin2θ成反比，因为给定的丸流随着θ的减小，会产生更大的撞击面积。

 

图8喷丸角度对凹坑尺寸和覆盖率的影响

    随着喷丸角度的减小，覆盖率的下降甚至快于喷丸强度。我们再一次有了实用意义——获得给定的覆盖率的时间较大程度的取决于喷丸角度。

凹坑体积

    不论是通过预测或实测凹坑的直径和深度，我们都可以预测其体积。圆形凹坑体积v为：

    V=(π/6)(3d2/4+h2)h      （4）

    凹坑体积是很重要的，因为它表征了丸料撞击在工件上的做功多少。丸料撞击在工件表面时具有动能1/2mv2。这说明丸料具有越大的动能，其产生的凹坑体积越大。

凹坑直径测量

    喷丸凹坑是非常小的，10~1000微米，因此在精确测量时放大镜是必需的。放大镜可以是单一的光学放大镜或是光学数字复合式的。

    我们可以通过直接的方法-使用光学影像，或是间接的方法-使用数字影像来测量凹坑直径。在直接测量时使用显微镜会使结果更准确。人类的每只眼睛有1亿2千5百万的视杆细胞来探测白色和黑色，有7百万视锥细胞来探测彩色。使用两只眼睛我们就有立体感的优势。而典型的数字相机仅有1千万的像素。

    测量技术有着较大的使用空间，每种都有优点和缺点。然而，每种技术依靠的都是刻度板。刻度板是一种小型的标尺，是在金属或玻璃板上采用精确的技术画有一定距离的线。典型的刻度板如图9所示，1毫米的距离被等分为100段。

 

 

图9公制刻度板——1毫米等分为100份

 

    为读者所喜欢的两种技术是基于使用测量显微镜或USB显微镜。图10所示为两种方法的差异。

 

 

图10 直接或间接测量凹坑尺寸

测量显微镜

    使用带有测量目镜的显微镜设备是比较容易确认尺寸的大小并比较容易存档。测量显微镜上的刻度是需要校验的。刻度用于测量凹坑，在放大镜下校验后，可以直接用于凹坑尺寸的检测。在目前的几种方法中，这种方法是最为精确且可靠的。它的主要缺点是不可携带性，因此在用于大工件上检测某一点的凹坑尺寸时具有局限性。

USB显微镜

    USB显微镜已经达到可以充分精确测量凹坑尺寸的阶段。当添加夹具时，可以较容易在实际工件喷丸面上聚焦，然而，一个重要的问题是必要的校准程序。作者提出了一个解决办法，如图11所示。

 

 

图11 Fig.11 Decal black dot on self-adhesive yellow labelstuck to peened component

 

    可粘贴黑点采用高精度工艺进行制作，其直径可以采用显微镜计数线或者测量显微镜进行测试。可以使用一个或多个黑点粘贴到自粘性胶带上，然后放入喷丸区域进行拍照。选取一个合适的放大镜对黑点和喷丸表面进行同时或者连续拍照。图11中的黑点直径为0.450mm（采用测量显微镜方法测出的结果），可以作为在电脑屏幕上评估凹坑尺寸的参考。或者采用0~100的显微镜计数线对黑点进行比对，一直找到和黑点直径相同的尺寸为止。然后采用该计数线和零件的凹坑尺寸进行对比。

 

总结                                                                                                         

 

    丸粒冲击后的凹坑的直径和面积可以由公式（3）进行预测。凹坑深度可以由公式（1）进行预测。这些预测需要知道一些喷丸的参数。喷丸或抛丸时丸料的飞行速度一般很难直径测试但是可以用公式（3）进行预测。凹坑尺寸的变化可能是由操作条件或者零件性能发生变化而引起的。

    对于特定尺寸的丸料而言，凹坑深度是与喷丸强度直接相关的。有一点是达成共识的，即喷丸强度是与阿尔门试片表面上的凹坑尺寸的大小相关，而非丸料尺寸的大小相关。对于任意已知直径的丸料，在其它条件不变的情况下，随着丸料直径的增加，凹坑深度也随之增减。这就引起了关于塑性变形的相关基础问题，目前需要相关试验进行验证。

    凹坑的平均面积A是影响覆盖率C的三个因素之一。其它的因素是凹坑增长速率（单位时间单位面积凹坑的数量），还有喷丸时间t。公式（5）给出了这三个参数之间的一个关系式。

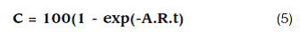
   其中，凹坑直径是影响覆盖率的首要因素。相关的计算机程序可以给出覆盖率和凹坑直径之间的相关预测。然而，所有的这些程序（包括本文中的等式）都是基于喷丸工艺理想模型的基础上的，这也就意味着虽然这些公式和程序很有用，但是却不能保证精确性。